Modeling Complex Fluid Flow in Porous Media Using Graph Neural Networks
S. T. Sathujoda, and S. Sheth
In European Conference on the Mathematics of Geological Reservoirs, Sep 2024
Carbon capture and sequestration initiatives make new demands on modern reservoir simulators. To find optimal locations and volumes of CO2 to inject into a subsurface to maximize CO2 storage, we must simulate a large ensemble of injection cases. One possible solution to the computational complexity of this task is to employ machine-learning models which, after a one-off overhead cost of training, can infer and predict future states of a reservoir several orders of magnitude faster than traditional methods.
Most previous work in the literature has primarily focused on either convolution-based methods or, more recently, neural operator-based methods, to predict the evolution of state variables. These architectures have shown promise in predicting on structured reservoir grids but lack the capability to extend the same level of accuracy to unstructured grids. Graph neural networks (GNNs) overcome this bottleneck by incorporating inductive biases arising from local messagepassing mechanisms, facilitating convolution operations over complex graphs and meshes.
In this work, we present a novel autoregressive GNN autoencoder to predict time-varying state variables for an ensemble of CO2 injection cases. We implement a graph convolution network for the message-passing protocol and incorporate physics-informed edge weights between cell connections to guide flow. An exhaustive set of node features are used to train the model on the hyperbolic evolution of phase saturations while preserving the ellipticity in the pressure.
We test the performance of the GNN model for (1) its ability to predict state variables for varying injection rates of CO2, (2) for the post-injection phase, and (3) under different unseen geological configurations. Training and testing are performed by constructing ensembles of 2D, 3D, and real field cases that best represent these scenarios. For the 2D regular grid case, we observe that the model can capture pressure and saturation values accurately, even for highly varying injection rates and with only a limited amount of data. This performance is maintained in the post-injection phase. A key advantage of GNNs is that they show a distinct ability for transfer learning on ensembles of unseen geological configurations. We observe that the model can predict the shape and intensity of wavefronts of certain cases with no prior exposure to the specific static properties during training. Similar results are produced for 3D grids and real field cases.
Coupled Graph Neural Network and Fourier Neural Operator Architecture for Ensemble Workflows in 3D Reservoir SimulationIn SPE Reservoir Simulation Conference, Mar 2025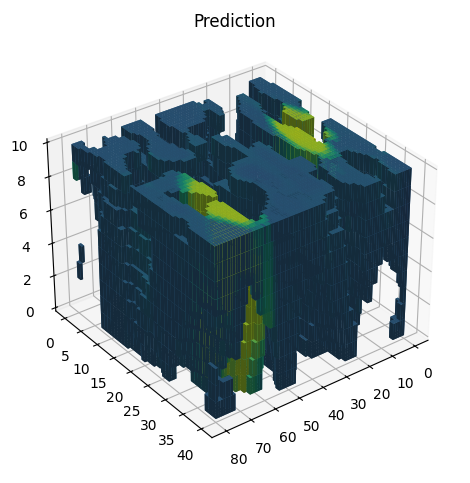
Modeling Complex Fluid Flow in Porous Media Using Graph Neural NetworksIn European Conference on the Mathematics of Geological Reservoirs, Sep 2024
